Examples

Here you find some short examples showing how quick and easy odeint can be used to implement numerical simulations. For a more detailed description please vist the docs.

- Lorenz System: 30 lines of C++ to generate a trajectory on the Lorenz attractor
- Simple 1D ODE : A small example showing the integration of a simple 1D system.

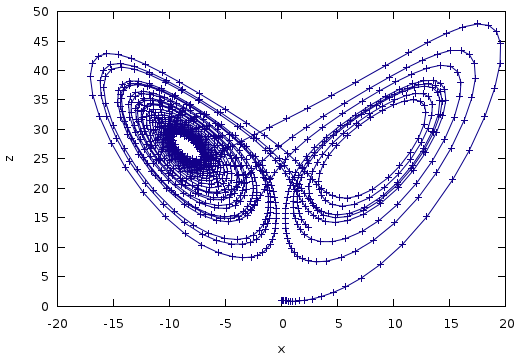
Lorenz System

30 lines of C++ to generate a trajectory on the Lorenz attractor.

#include <iostream>
#include <boost/array.hpp>

#include <boost/numeric/odeint.hpp>

using namespace std;
using namespace boost::numeric::odeint;

const double sigma = 10.0;
const double R = 28.0;
const double b = 8.0 / 3.0;

typedef boost::array< double , 3 > state_type;

void lorenz( const state_type &x , state_type &dxdt , double t )
{
    dxdt[0] = sigma * ( x[1] - x[0] );
    dxdt[1] = R * x[0] - x[1] - x[0] * x[2];
    dxdt[2] = -b * x[2] + x[0] * x[1];
}

void write_lorenz( const state_type &x , const double t )
{
    cout << t << '\t' << x[0] << '\t' << x[1] << '\t' << x[2] << endl;
}

int main(int argc, char **argv)
{
    state_type x = { 10.0 , 1.0 , 1.0 }; // initial conditions
    integrate( lorenz , x , 0.0 , 25.0 , 0.1 , write_lorenz );
}

go to top

Simple 1D ODE

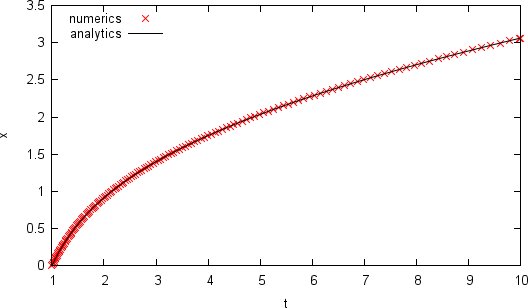
The following code shows how to obtain the numerical solution of a simple one-dimensional ODE. Note the configuration of the stepper type showing the flexibility of the library.

#include <iostream>
#include <boost/numeric/odeint.hpp>


using namespace std;
using namespace boost::numeric::odeint;


/* we solve the simple ODE x' = 3/(2t^2) + x/(2t)
 * with initial condition x(1) = 0.
 * Analytic solution is x(t) = sqrt(t) - 1/t
 */

void rhs( const double x , double &dxdt , const double t )
{
    dxdt = 3.0/(2.0*t*t) + x/(2.0*t);
}

void write_cout( const double &x , const double t )
{
    cout << t << '\t' << x << endl;
}

// state_type = double
typedef runge_kutta_dopri5< double > stepper_type;

int main()
{
    double x = 0.0;    
    integrate_adaptive( make_controlled( 1E-12 , 1E-12 , stepper_type() ) ,
                        rhs , x , 1.0 , 10.0 , 0.1 , write_cout );
}

go to top